ریاضی در معماری

«معماران، مهندسانی هستند که ریاضی بلد نیستند».

حتماً شما تا به حال چنین جملاتی شنیده‌اید که چندان درست نیستند.

اگر شما در حال برداشتن قدم‌های اولتان در زمینه معماری هستید، فریب این ادعاها را نخورید.

شما قطعاً به ریاضیات نیاز خواهید داشت.

معماران هم از ریاضیات استفاده می‌کنند ولی ممکن است کاربرد آن‌ها کمی متفاوت با رشته‌های دیگر باشد.

بعضی افراد می‌گویند ریاضیات معماران ساده است.

آن‌ها احتمالاً چیزی از نسبت طلایی و طراحی پارامتریک نشنیده‌اند.

 با پیشرفت سریع ابزارهای مدل‌سازی و طراحی مفهومی؛

داشتن دانش ریاضی می‌تواند شما را در موقعیت بهتری قرار دهد.

آیا معماران باید در ریاضیات خوب باشند؟

پاسخ این است که معماران باید به جای اینکه در ریاضیات خوب باشند ، خوب باشند.

هیچ وجهی وجود ندارد که وانمود کنیم این یک قسمت اساسی کار نیست،

اما همچنین به ندرت پیش می آید که شما از هر چیزی دشوارتر از

ریاضی در معماری دبیرستان استفاده کنید:

جمع ، تفریق ، ضرب ، تقسیم ، معادلات ، هندسه (کار با خطوط ، زاویه ها سطح و جامدات) ، و مثلثات (کار با روابط بین طول اضلاع و زاویه های مثلث).

معماران مسلماً از مواردی مانند حساب (کار با نرخ تغییر) به صورت روزمره استفاده نمی کنند.

معماران به جای مهارت در ریاضی به خودی خود ، باید در تفکر ریاضی مهارت داشته باشند.

شما باید بدانید که چگونه مشکلات را با اعداد حل کنید.

خوشبختانه امروز ما از فناوری برخوردار هستیم که حل واقعی را برای ما انجام می دهد.

و استفاده از ریاضیات در دنیای حرفه ای همان استفاده از ریاضیات در کلاس نیست،

زیرا در استودیو دلایل عملی برای محاسبات وجود دارد.

قطعات این ساختمان به درستی در کنار هم قرار می گیرند؟

فضای کافی برای قرار دادن درب دیگری در اینجا وجود دارد؟

پله راحت به طبقه بعدی خواهد رسید؟

اینها شرایطی است که معماران باید به طور ریاضی فکر کنند.

پنج دلیلی که معماران به ریاضیات نیاز دارند؟

۱. تبدیل واحد

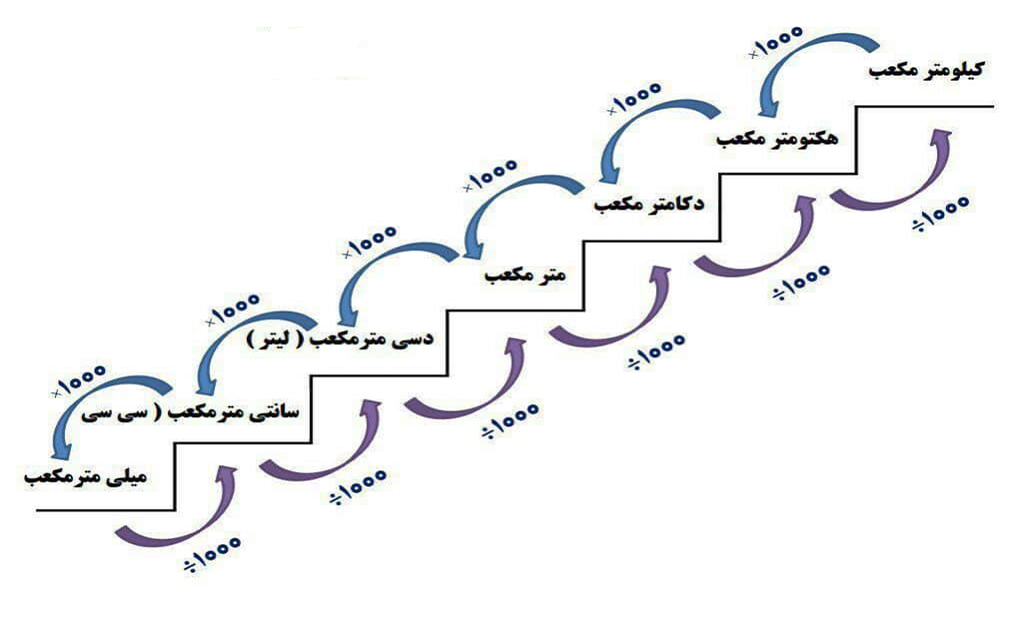
این از ابتدایی‌ترین کارها در معماری است که نیاز به دانش مقدماتی ریاضیات دارد.

معماران بیشتر با مساحت و ارتفاع سر و کار دارند.

اگر شما جزو اکثریتی هستید که با سیستم متریک کار می‌کنید،

باید بتوانید سانتی متر را به متر و متر را به کیلومتر تبدیل کنید و

همین‌طور مساحت را به دست آورید و از

سانتی متر مربع به متر مربع و یا متر مربع به هکتار تبدیل کنید.

اگر سیستم شما آمریکایی است باید بتوانید اینچ را به فوت و فوت

را به مایل تبدیل کنید و همین‌طور برای مساحت، فوت مربع را به جریب تبدیل نمایید.

اگر پروژه‌ای که در دست دارید بین‌المللی است، باید با تبدیل واحد در هر

دو سیستم آشنا باشید و به طور مثال بتوانید فوت را به متر، مایل را به کیلومتر و جریب را به هکتار تبدیل کنید.

 ۲. به مقیاس درآوردن

از اولین کارهای یک دانشجوی معماری کشیدن پلان با

مقیاس ۱ به X است که X می‌تواند ۵۰، ۱۰۰ یا ۲۰۰ باشد.

هر چه مقیاس بزرگ‌تر باشد، به جای ساختمان می‌توان یک محله یا

شهر را نمایش داد و X می‌تواند ۱۰۰۰ یا ۲۰۰۰ باشد؛ اما ۱ و X به چه معنا هستند؟

۱ واحد طول در ترسیم است که بیانگر طول X در دنیای واقعی است.

به عنوان مثال در سیستم متریک مقیاس ۱ به ۱۰۰ به این معناست که هر

100 سانتی متر در واقعیت، در نقشه ۱ سانتی متر نشان داده شده است.

محاسبه ابعاد ترسیم به مقیاس مد نظر، نیاز به آشنایی با واحدها و استفاده از تناسبات دارد.

 ۳. سازگار کردن تناسبات

داشتن تناسبات مطلوب برای موفقیت هر طراحی از جمله طراحی معماری حیاتی است.

دلیل این است که معماران و طراحان از زمان‌های گذشته سعی در پی بردن به

تناسب کامل برای یک ترکیب هنری (یا کمپوزیسیون) یا طراحی یک ساختمان بی‌نقص داشتند.

تناسب‌ها، نسبت بین اعداد هستند و درک آن‌ها نیاز به دانش ریاضی دارد.

مشهورترین نسبت که به طور گسترده‌ای در معماری مورد استفاده است، نسبت طلایی می‌باشد.

نسبت طلایی برابر است با ۱:۱.۶۱۸.

نسبت طلایی ارتباطی قوی با آنچه به عنوان اعداد فیبوناچی (۰، ۱، ۱، ۲، ۳، ۵، ۸، ۱۳، ۲۱، ۳۴…) شناخته می‌شوند، دارد.

۴. نوشتن صورتحساب مقادیر

صورتحساب مقادیر لیست کاملی از اجزای ساختمان است.

برای مثال مقدار آجر، مقدار قاب پنجره آلومینیومی، مقدار رنگ و مقدار کاشی سرامیکی.

هر چیزی که در بنا استفاده شده است باید در لیست بیاید و برای نوشتن آن به ریاضیات نیاز است.

باید بدانید چگونه پارامترها، مساحت‌ها و حجم‌ها را محاسبه کنید و آن‌ها را به مبلغ تبدیل کنید.

۵. ساختن فرم‌های پیچیده و عملکردی

تنها با طراحی پارامتریک می‌توان به چنین فرم‌هایی دست یافت.

طراحی پارامتریک روشی است که الگوریتم‌هایی با مجموعه‌ای از

متغیرها یا پارامترها را به کار می‌گیرد تا فرم‌های هندسی منحصر به فردی تولید کند.

تمامی اجزای مختلف سازه معماری به صورت مؤلفه‌های ریاضی تعریف می‌شوند که

می‌توان آن‌ها را اصلاح کرد و به معادلات و عملیات ریاضی تبدیل نمود.

هر چه معمار بیشتر در هندسه، مکانیک و ریاضی دانش داشته باشد،

بیشتر می‌تواند در ابزارهای طراحی پارامتریک دست‌کاری کند و محصول ویژه‌ای تولید نماید.

از نمونه‌های مشهور معماری که در طراحی آن‌ها ریاضیات پیچیده به کار رفته است می‌توان به تالار کنسرت والت دیسنی با

طراحی فرانگ گری، مرکز حیدر علی اف با طراحی زاها حدید و برج خیار شور لندن با طراحی فاستر اشاره کرد.

در واقع، مدت‌ها قبل از اینکه طراحی پارامتریک به عنوان روش رایج قرن شناخته شود،

معمار معروف اسپانیایی آنتونیو گائودی طراح کلیسای ساگرادا فامیلیا،

روش مشابهی در طراحی معرفی کرد که ساز و کاری مشابه با طراحی پارامتریک داشت.

چگونه ریاضیات با معماری ارتباط دارد؟

ما بدون ریاضیات نمی توانستیم معماری بسازیم.

گاهی اوقات ، معماران ریاضیات را قابل مشاهده می کنند –

در مورد ساختمان ” Gherkin ” لندن توسط Foster + Partners یا

دفتر مرکزی دوربین مداربسته توسط Rem Koolhaas و Ole Scheeren در پکن فکر می کنند

– در حالی که بار دیگر ، محاسبات طراحی ساختمان را به

صورت قائم نگه می دارند نه دیده می شوند و نه مورد ارزیابی قرار می گیرند.

معماری دینی از زمان های بسیار قدیم ، اغلب به دلایل نمادین ، ​​به ریاضیات متکی بوده است.

به عنوان مثال ، بسیاری از معابد هندو در هند دارای ساختارهای نمادین،

​​مانند فراکتال هستند که در آنها اجزای سازنده شکلی مشابه کل دارند.

در طراحی سکولار نیز زیبایی شناسی معماری مدت هاست که توسط ریاضی در معماری پشتیبانی می شود.

اولین کتاب در زمینه معماری که تاکنون منتشر شده است،

“Alberti On the Art of Building” (۱۴۵۰)، دیدگاه خطی را توضیح داد

و نظرات نویسنده را در مورد اشکال مورد پذیرش و اجتناب از آنها ارائه داد.

اصول ریاضی برای معماری

اصول ریاضی اصول اصلی ریاضیات است که ما هر وقت وظیفه خاصی را

انجام می دهیم از آنها استفاده می کنیم.

شاید فکر نکنید که قبلاً با آنها روبرو شده اید،

اما اگر به شما ترتیب مقابله با قسمت هایی از یک معادله

یعنی براکت ها ، شاخص ها ، ضرب ، تقسیم ، جمع ، تفریق – به شما آموزش داده شود،

در این صورت می فهمید که یک اصل ریاضی چیست.

ما برای حل هر معادله از همین قانون استفاده می کنیم ، به همین دلیل به شما گفته شد

قبل از آن آزمون ۵۰ بار “BIMDAS” را تکرار کنید!

در همین راستا ، برخی اصول ریاضی در معماری بارها و بارها در معماری رخ می دهد.

تناسب – نسبت طلایی و توالی فیبوناچی

در بالا دیدیم که استفاده از نسبت طلایی (۱: ۱.۶۱۸) منجر به نسبت هماهنگ بصری در معماری می شود.

به همین ترتیب ، توالی فیبوناچی (۱ ، ۲ ، ۳ ، ۵ ، ۸ ، ۱۳ و غیره – هر عدد مجموع دو مورد قبلی است)

در بسیاری از زیباترین بناهای جهان دیده می شود.

نسبت طلایی و توالی فیبوناچی از نزدیک با هم مرتبط هستند.

بعد از ۱۳ در توالی فیبوناچی ، هر عدد به ۱.۶۱ بار بعدی تقسیم می شود!

خطوط عمود

خطوط عمود خطوطی هستند که در زاویه های راست به هم می رسند.

به عنوان یک معمار ، شما می آموزید که چگونه اینها را با خط کش ، مداد و قطب نما کاملاً ترسیم کنید.

خطوط موازی

خطوط موازی نیز نه تنها در نقشه های معماری بلکه در خود ساختمان ها نیز ضروری هستند.

حتی در زیر ارگانیک ترین اشکال گائودی سازه هایی

وجود دارد که برای ایستادن به خطوط موازی متکی هستند.

چگونه ریاضیات بر ساختمان ها تأثیر می گذارد؟

به طور خلاصه ، ساختمانها تحت تأثیر آنچه از نظر ریاضی امکان پذیر است ، هستند.

به عنوان مثال ، وزن به طور کلی در پایین ساختمان متمرکز می شود تا از سقوط جلوگیری کند،

اگرچه موارد استثنایی در این قانون وجود دارد مانند ساختمان رادیوی

اسلواکی یا کتابخانه پکهام لندن که به نظر می رسد از جاذبه سرپیچی می کند!

ریاضیات همچنین به ما کمک می کند معماری سازگارتر با محیط زیست تولید کنیم.

سالن شهر لندن را در نظر بگیرید که به دلیل شکل ناهموار اما تقریباً کروی آن،

با چراغ جلو و بیضه مقایسه شده است.

تالار شهر به این صورت طراحی شده است که سطح کره ها در مقایسه با حجم آنها سطح کمی دارد،

به این معنی که گرما برای ساختمان در زمستان کمتر است.

همچنین در تابستان هزینه کمتری برای خنک شدن دارد،

زیرا پنجره های طبقه فوقانی در ضلع جنوبی سایه ای برای کف های زیر ایجاد می کنند.

یک نوآوری (نسبتاً) اخیر که درک بهتری از آنچه در معماری از نظر ریاضی در

معماری امکان پذیر است به ما داده است، مدل سازی پارامتریک است.

اکنون یک ویژگی مشترک نرم افزار CAD، ابزارهای مدل سازی پارامتریک به

کاربر این امکان را می دهد تا ضمن ثابت نگه داشتن دیگران ، یک جنبه از طراحی ساختمان را تغییر دهد.

به عنوان مثال ، اگر قطعه ای با اندازه ثابت دارید که می توانید روی آن احداث کنید،

می توانید آن ابعاد را قفل کنید و با طول یک کانتینر بالقوه بازی کنید تا

زمانی که به نقطه اوج – به معنای واقعی کلمه – برسد.

نمونه هایی از ریاضیات در معماری

اگر به دنبال الهام – یا فقط یک شواهد کوچک هستید که

ریاضیات باعث ایجاد زیبایی و همچنین سردردهای تنشی می شود

۱۰ ساختمان برتر الهام گرفته از ریاضیات را بررسی کنید.

۱. هرم بزرگ جیزه ، قاهره ، مصر (۲۵۶۰-۲۵۶۰ قبل از میلاد)

انواع اسرار ریاضی در این هرم باستانی که قبلاً بلندترین سازه ساخته شده توسط

بشر در جهان بوده است، کشف شده است.

ریاضی در معماری اگر با یک چرخ چرخ در پایه حرکت کنید،

می بینید که ۳۶۵.۲۴ ذراع محیط است که با تعداد روزهای سال مطابقت دارد

(یک مکعب واحد طول مصری ها بود که اندازه آن کمتر از نیم متر بود) .

علاوه بر این ، اگر محیط را به دو برابر ارتفاع هرم تقسیم کنید ، جواب ۳.۱۴۱۶ یا pi است.

۲. پارتنون ، آتن ، یونان (۴۴۷-۴۳۲ قبل از میلاد)

برخی از محققان استدلال کرده اند که پارتنون بر اساس نسبت طلایی بنا شده است.

این دقیق باشد یا نباشد ، نسبت عرض به طول آن ۴: ۹ است که نسبت های

مطابق با سلیقه کلاسیک را منعکس می کند.

همچنین شواهد واضحی در پارتنون وجود دارد که یونانیان نحوه عملکرد توهمات نوری را درک کرده اند.

نما شش سانتیمتر در مرکز نسبت به کناره ها بلندتر است و ستون ها در وسط متورم می شوند.

هر دو تصور تحریف شده چشم انسان را “اصلاح” می کنند و ساختمان را صاف نشان می دهند!

۳. چیچن ایتزا ، یوکاتان ، مکزیک (۷۰۰-۱۱۰۰ پوند)

تعجب آور نیست که تمدن مسئول مفهوم صفر نیز یکی از شگفتی های معماری جهان را ایجاد کرده است.

چیچن ایتزا شهری بود که بر اساس اصول ریاضی در معماری ساخته شده است:

به عنوان مثال معبد کوکولکان ، در مرکز ، دارای ۵۲ صفحه در هر طرف (هر یک از آنها برای هر سال از چرخه مایان).

۱۸ طبقه (برای هر ماه از سال تولید مایا) و ۳۶۵ قدم در داخل آینه آن قرار دارد (برای هر روز از سال خورشیدی یک قدم).

۴. ویلا کاپرا ، ویچنزه ، ایتالیا (۱۵۶۷-۱۵۹۲)

آندره پالادیو تحت تأثیر سبک یونان و روم باستان قرار گرفت و در رساله خود، 

چهار کتاب معماری ، تفسیرهای دوره رنسانس را از ایده آل های کلاسیک گسترش داد .

 تمام ساختمان های پالادیو تعادل و هماهنگی را نشان می دهند که تقریباً شدید احساس می شود،

اما ویلا کاپرا وی کاملاً قرینه با یک نقشه مربع، چهار رواق برجسته و یک سالن

دایره ای شکل مرکزی است که بالای آن گنبدی قرار دارد.

۵. تاج محل ، آگرا ، هند (۱۶۳۲-۵۳)

تاج محل بر روی شبکه های درون شبکه ای طراحی شده است،

و هر عنصر به طور دقیق چیده شده است.

زاویه ، وزن و اندازه مناره ها برای محافظت از آنها در برابر زلزله، با استفاده از روش

دانش هندسی پیش از زمان خود محاسبه شد و این ساختمان اغلب

به عنوان بنای یادبود تقارن مورد ستایش قرار می گیرد.

ریاضی در معماری داخل آن ، رسوبات نقاشی و نقش و نگارهای دیگر روی کف

و دیوارها نشان می دهد که مغول ها چقدر به هماهنگی بصری اهمیت می دهند.

۶. گنبدهای ژئودزیک ، مکان های مختلف (۱۹۲۶-)

به نظر می رسد گنبدهای ژئودزیک مثلثی پوشیده شده اند،

زیرا از ژئودزیک های متقاطع ساخته شده اند.

کوتاهترین خطوط بین دو نقطه روی یک سطح منحنی.

فرض بر این است که آنها معمولاً زاییده ایده معمار آمریکایی باکمینستر فولر هستند،

اما در واقع این یک آلمانی بود ، والتر بائورسفلد ، که اولین بار این ایده را داشت.

در انگلستان ، گنبدهای ژئودزیکی را می توانید در Eden Project در Cornwall مشاهده کنید.

۷. خانه های مکعب ، روتردام / هیرمند ، هلند (۱۹۷۷)

خانه های پیت بلوم به شکلی شبیه درخت طراحی شده اند.

ستون های شش ضلعی نمایانگر تنه ها هستند ،

در حالی که بالای کوهها مکعبی هستند که به زاویه ای بیش از ۴۵ درجه تبدیل شده اند.

خانه های با ظاهری غیرقابل باور نماهای خارق العاده ای دارند اما به دلیل

کمبود فضای موجود در آن مورد انتقاد قرار گرفته اند.

اگر خود را در روتردام می بینید ، یکی از ساکنان مکعب خود را برای عموم باز کرده است.

۸. موزه گوگنهایم ، بیلبائو ، اسپانیا (۱۹۹۷)

اعتبار بخشیدن به اقتصاد بیلبائو به گوگنهایم از فرانک گری گفته شده است

و درک اینکه چرا بازدیدکنندگان فقط برای دیدن آن سفرهای بین المللی را انجام می دهند آسان است.

این ساختمان مجموعه ای متنوع از اشکال، که به نظر می رسد

در مقیاس های براق کننده ماهی پوشانده شده است

ریاضی در معماری به لطف پیشرفت در نرم افزار مدل سازی در اواخر دهه ۹۰،

مانند هر چیزی که موجود بود نبود.

انجام محاسبات لازم برای ساخت گوگنهایم فراتر از بیشتر انسان ها خواهد بود،

اما اکنون فناوری در حال ایجاد معماری به ظاهر غیرممکن در تصویر موزه است.

۹. مرکز فرهنگ و هنر بین المللی ، چانگشا ، چین (۲۰۱۹)

دو دهه پس از افتتاح گوگنهایم ، معماران Zaha Hadid اصول خود را یک قدم جلوتر بردند

و این مرکز هنری سه بخشی ارگانیک را ایجاد کردند که به نظر می رسد خمیردندان از لوله خارج می شود.

۱۰. “معبد موبیوس” ، تایکانگ ، چین

نوار موبیوس ، بدون آغاز و پایان ، نه داخل و خارج ، الهام بخش یک معبد بودایی جدید در شرق چین است.

شکل نامحدود نوار نماد اعتقاد بوداییان به یگانگی ابدی جهان است

و می توانید طرح پیشنهادی (توسط Miliy Architects) را در اینجا مشاهده کنید.